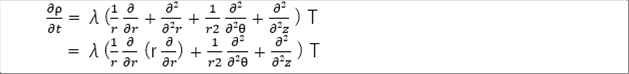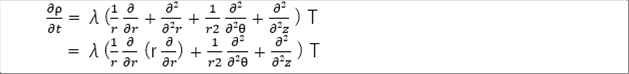| |
 |
| |
 |
| 仠丂墌拰嵗昗宯傪巊偆偲曋棙側応崌 |
| 仠丂擬揱摫曽掱幃堦斒幃 |
| 仠丂懱愊偲擬棳検 |
| 丂丂倰曽岦偺擬僶儔儞僗 |
| 丂丂兤曽岦偺擬僶儔儞僗 |
| 丂丂z曽岦偺擬僶儔儞僗 |
| 丂丂慡懱偺擬僶儔儞僗 |
| 仠丂擬揱摫曽掱幃偺傑偲傔 |
| 仠丂摿堎揰偺埖偄丂倰亖侽乮拞怱幉乯 |
| 仠丂嵎暘昞尰乮徻嵶偼嵎暘嶲徠乯 |
| 仠丂僔儈儏儗乕僔儑儞乮徻嵶偼僔儈儏儗乕僔儑儞嶲徠乯 |
| |
 |
| 仠丂墌拰嵗昗宯傪巊偆偲曋棙側応崌 |
| |
| 丂擬揱摫曽掱幃偺堦斒宍幃偼偳偺嵗昗宯偵傕揔梡偱偒傞丅壏搙僔儈儏儗乕僔儑儞偺偨傔偵偼丄昁梫側嵗昗宯偵曄姺偡傟偽偄偄丅斅偼捈岎嵗昗丄娵峾曅乮價儗僢僩乯丄僷僀僾偼墌摏嵗昗偑揔偟偰偄傞偲巚傢傟傞丅 |
| |
 |
| 仠丂擬揱摫曽掱幃堦斒幃 |
| |
| 丂擬揱摫曽掱幃偺堦斒幃偼師幃偱梌偊傜傟傑偡丅 |
| |
 |
| 丂 佪兿/佪倲 = 兩嚈T, 兿=CvT |
| |
| 墌拰嵗昗偱偼丄師偺傛偆偵側傝傑偡丅 |
| |
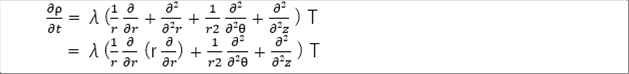 |
| |
| 丂幃偼巊偊傟偽偄偄偺偱偡偑丄摫弌偺曽朄偑棟夝偱偒傞偲庴偗擖傟傗偡偄偲巚偄傑偡丅偙偙偱偼擬偺棳傟偐傜擬揱摫曽掱幃傪摫弌偟傑偡丅 |
| |
 |
| 仠丂旝彫懱愊偱偺擬棳検 |
| |
| 丂墌拰嵗昗偱偺旝彫椞堟偱偺懱愊偼師幃偱梌偊傜傟傑偡丅 |
| |
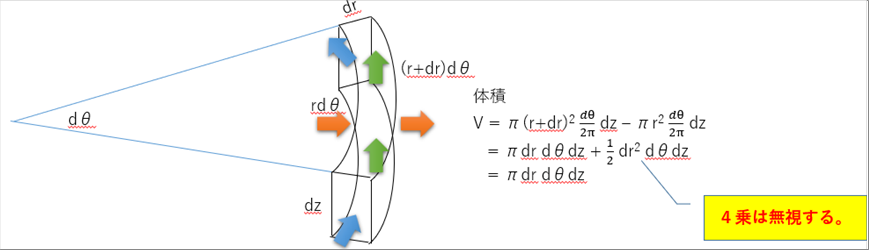 |
| |
| 丂旝彫椞堟側偺偱丄4忔偼柍帇偟偰偄傑偡丅偦偆偡傞偲丄捈岎嵗昗偲傎傏摨偵昞尰偱偒傑偡丅 |
| |
| 丂偙偙偱丄栴報偼擬僄僱儖僊乕偺棳傟傪昞偟偰偄傑偡丅捈岎嵗昗偲摨偠偔丄僼乕儕僄偺朄懃乮擬棳偼丄壏搙岡攝偵斾椺偡傞丅乯傪揔梡偱偒傑偡丅 |
| |
 |
| |
| 兤曽岦偼梫拲堄偱丄嫍棧偵懳偡傞曄壔棪側偺偱丄倓兤偱偼側偔倰倓兤偲側傝傑偡丅 |
| |
 |
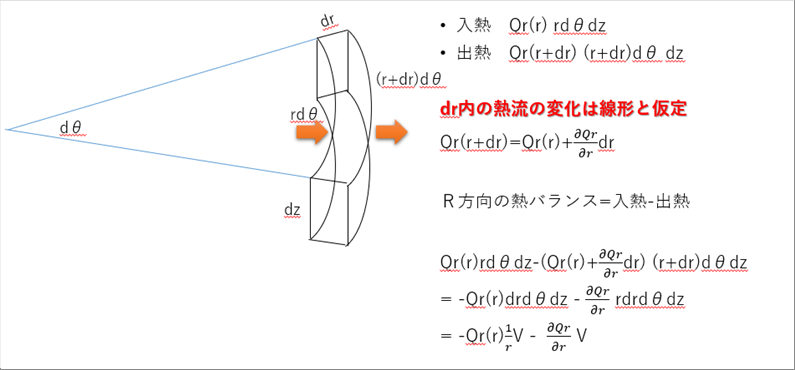
| 仠丂倰曽岦偺擬僶儔儞僗 |
| |
 |
| |
| 旝彫椞堟側偺偱丄擬僄僱儖僊乕偺曄壔偼丄旝彫椞堟撪偱偼嫍棧偲斾椺娭學偵偁傞偲偟傑偡丅乮俀師埲忋偺暋嶨側娭學偱偼側偄偲壖掕偟偰偄傑偡丅乯 |
| |
 |
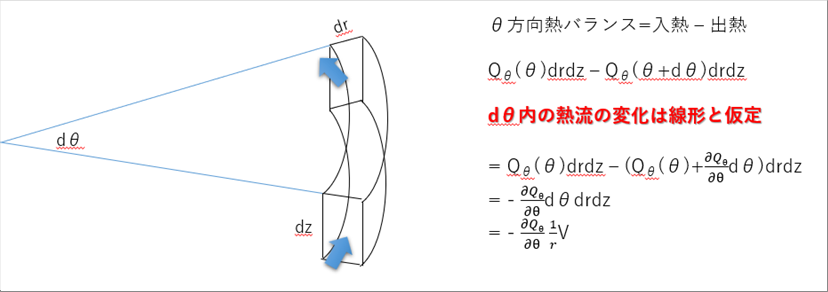
| 仠丂兤曽岦偺擬僶儔儞僗 |
| |
 |
| |
| 丂旝彫椞堟側偺偱丄擬僄僱儖僊乕偺曄壔偼丄旝彫椞堟撪偱偼嫍棧偲斾椺娭學偵偁傞偲偟傑偡丅乮俀師埲忋偺暋嶨側娭學偱偼側偄偲壖掕偟偰偄傑偡丅乯 |
| |
 |
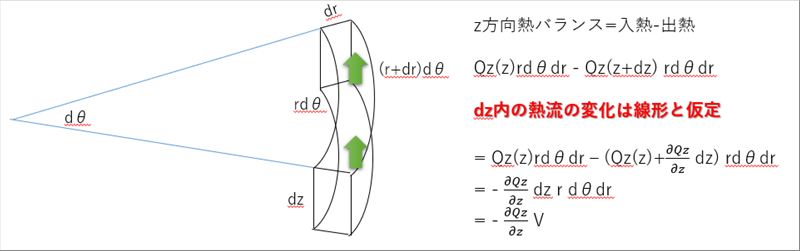
| 仠丂z曽岦偺擬僶儔儞僗 |
| |
 |
| |
| 旝彫椞堟側偺偱丄擬僄僱儖僊乕偺曄壔偼丄旝彫椞堟撪偱偼嫍棧偲斾椺娭學偵偁傞偲偟傑偡丅乮俀師埲忋偺暋嶨側娭學偱偼側偄偲壖掕偟偰偄傑偡丅乯 |
| |
 |
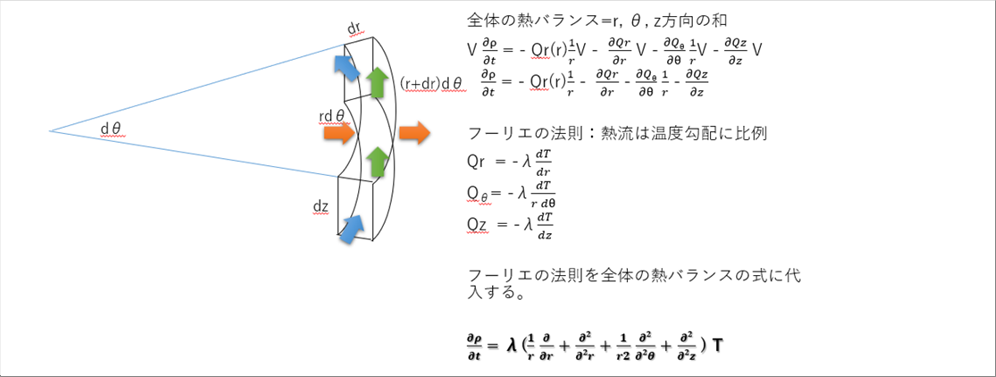
| 仠丂慡懱偺擬僶儔儞僗 |
| |
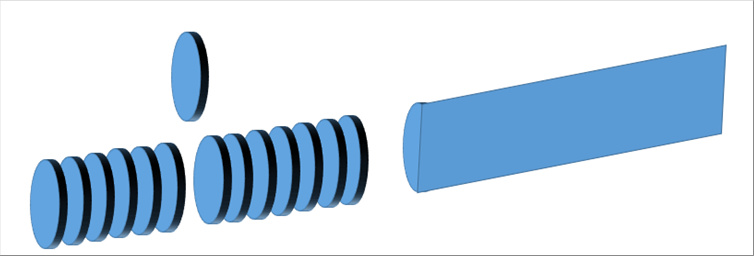
| 丂倰丄兤丄倸曽岦偺擬僄僱儖僊乕僶儔儞僗傪傑偲傔傞偲嵟弶偺奊偵側傝傑偡丅 |
| |
 |
| |
| 丂僫僽儔墘嶼巕傪巊偆偲丄捈岎嵗昗傕墌拰嵗昗傕摨偠幃偱丄偐偮娙曋偵昞尰偱偒傑偡丅 |
| |
 |
| 仠丂擬揱摫曽掱幃偺傑偲傔 |
| |
 |
| |
| 戞堦崁偲戞擇崁偵旝暘偺岞幃丂(fg)乫=f乫g+fg乫丂傪偁偰偼傔傞偲師幃偵側傝傑偡丅 |
| |
 |
| |
| 兿亖CvT側偺偱丄壏搙僔儈儏儗乕僔儑儞傪偡傞嵺偵偼師幃傪巊偆傎偆偑曋棙偱偡丅 |
| |
 |
| |
| 丂偙偙偱丄兛偼擬奼嶶學悢偲屇偽傟傞學悢偱偡丅 |
| |
 |
| 仠丂摿堎揰偺埖偄丂倰亖侽乮拞怱幉乯 |
| |
| 丂墌拰嵗昗偱偼丄拞怱幉偼摿堎揰偵側傝傑偡丅墌偱偼側偔懭墌偱嬤帡偡傞偲摿堎揰傪夞旔偱偒傞傛偆偱偡偑丄偙偙偱偼妱垽偟傑偡丅 |
| |
| 丂拞怱幉偼丄悢妛揑偵偼摿堎揰偱偡偑丄幚柋偱偼丄拞倰亙亖侽丏侽侾偲峫偊傞偲丄傎傏柍帇偟偰傕栤戣側偄偺偱偼側偄偐偲巚傢傟傑偡丅 |
| |
| 丂倰=0.01偲偟偨応崌丄奜宎100偱偼柺愊斾棪0.000001%側偺偱丄幚柋忋栤戣側偄偲巚傢傟傑偡丅偙偺掱搙偑栤戣偵側傞応崌偼丄摿堎揰偑偁傞墌拰嵗昗偼揔梡偟側偄傎偆偑偄偄偲巚偄傑偡丅 |
| |
 |
| 仠丂嵎暘昞尰乮徻嵶偼嵎暘嶲徠乯 |
| |
| 丂墌拰嵗昗偺擬揱摫曽掱幃傪拞怱嵎暘宍幃偱昞尰偡傞偲師幃偲側傝傑偡丅乮徻嵶偼嵎暘朄嶲徠乯 |
| |
 |
| |
 |
| 仠丂僔儈儏儗乕僔儑儞乮徻嵶偼僔儈儏儗乕僔儑儞嶲徠乯 |
| |
| 丂偁傞帪崗偺壏搙暘晍偑傢偐偭偰偄傞応崌丄旝彫帪娫嚈倲屻偺壏搙暘晍偼忋偺幃偱寁嶼偱偒傑偡丅偙傟傪弴師寁嶼偟偰偄偗偽丄抦傝偨偄帪崗偺壏搙暘晍偑寁嶼偱偒傑偡丅乮寁嶼椺偼丄僔儈儏儗乕僔儑儞嶲徠乯 |
| |
 |
| |
| 丂偁傞埵抲偺抐柺偺壏搙暘晍傪抦傝偨偄応崌偼丄娙堈朄偲偟偰倸偺崁傪柍帇偟偰倰丄兤偺傒偺幃偲偟偰寁嶼偟偰傕偄偄偲巚偄傑偡丅 |
| |
| Author: T. Oda |
| 偙偺儁乕僕偼僄僋僙儖偱嶌傝丄excel2web偱html偲css傪帺摦嶌惉偟傑偟偨丅 |