| |
 |
| |
 |
| (1) Air Used in the Manufacturing Plants |
| (2) Physical Properties of Air |
| (3) Temperature Dependence of Viscosity and Kinetic Viscosity |
| (4) Temperature Dependence of Specific Heat, Heat Convection, and Thermal Diffusivity |
| (5) Regression Equations |
| (6) Temperature Dependence of Prandtl Number |
| (7) Evaluation of the Regression Equations, Density, Thermal Diffusivity and Viscosity |
| (8) Evaluation of the Regression Equations, Specific Heat |
| |
| |
 |
| (1) Air Used in the Manufacturing Plants |
| |
| When we line normal lives, the air exists literally like air, and we do not pay attention. It is utilized everywehre in the manufacturing plants as well, such as for the blowing dusts, for the aspirator, for the pneumatic system, for the burners with fuel in order to heat steel sheets or pipes. |
| |
| When the air is used in the industry, it is important to know the characteristics by temperature. When we use it in the pneumatic system, or when we use it as a medium that transfers heat, the characteristics at the operating temperature is very important. |
| |
| The air is the mixture of nitroge, oxygen and other components. It is a gas at the room temperature, and it bocomes liquid at very low temperature, finally it becomes solid at fifty four (54) K. In teh usual manufacturing plants like the seamless pipe mills, the air is used at gas state. The characteristics of gas air varies by temperature, therefore, it is necessary to use the correct values. |
| |
| The characteristic or the property of air includes viscosity, specific heat, viscosity, kinetic viscosity, thermal conductivity, thermal diffusivity, and Prandtl number. There are many names and you may be got lost, but all of these are very important for the fluid dynamics and the thermodynamics. Please just remember that there are many temperature dependence indexes in the air. |
| |
| The physical properties of water are also temperature dependent and therefore it is important to pay attention when you do something for the heat exchanger, for example. Let's focus on the air here. |
| |
 |
| (2) Physical Properties of Air |
| |
| Out of the seven (7) physical properties of air, there are only four (4) are independent values. They are density, specific heat, viscosity, and convection heat transfer coefficient. We can calculate the rest of the physical characteristics. |
| |
 |
| |
| Please see "Flow Dynamics" and "Thermodynamics" for detail. |
| |
 |
| (3) Temperature Dependence of Viscosity and Kinetic Viscosity |
| |
| There are many open papers or web pages for the viscosity and the kinetic viscosity by temperature. As far as I know, there are small differences, but which to choose is out of scope here. The following graph shows not for the evaluation of the values but for the formulation for use in the calculations. |
| |
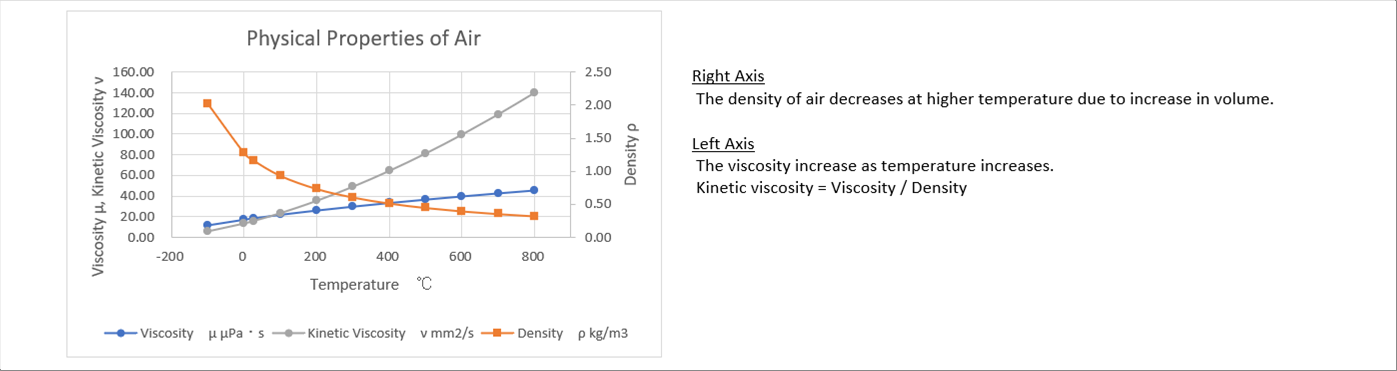 |
| |
| The density of air reduces as temperature rises, because the volume becomes bigger. Both of the viscosity and the kinetic viscosity increases. The degree of increase of the kinetic viscosity is bigger than that of viscosity, because it is affected by the reduction of density. |
| |
 |
| (4) Temperature Dependence of Specific Heat, Heat Convection, and Thermal Diffusivity |
| |
| The following graph shows the temperature dependence of the specific heat, convection heat transfer coefficient, and thermal diffusivity. |
| |
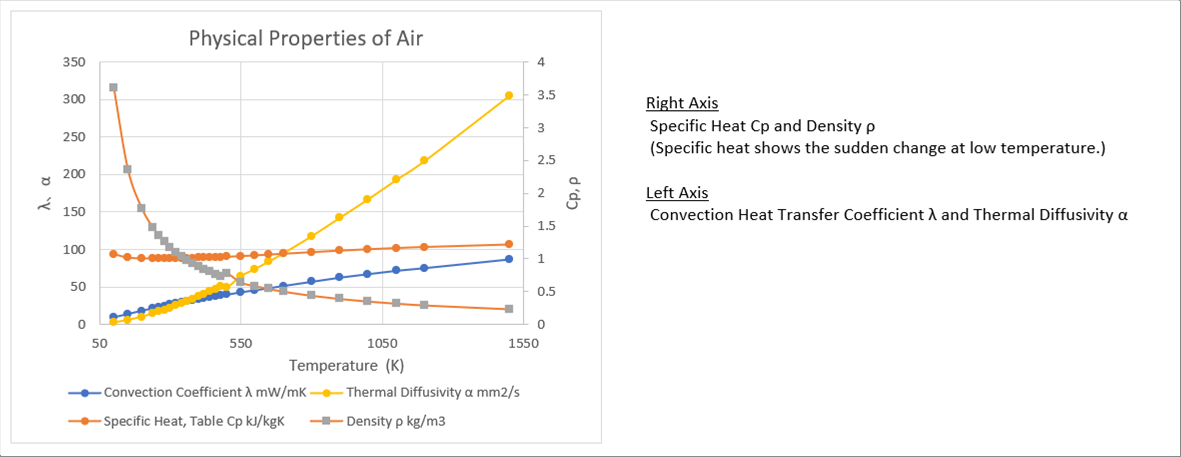 |
| |
| The specific heat changes a little, it reduces and then increases. The convection heat transfer coefficient increases as the temperature increases. The thermal diffusivity, which is defined as convection heat transfer coefficient divided by density and by specific heat, increases as temperature increases. |
| |
 |
| (5) Regression Equations |
| |
| The advantage of the regression equations is that we can calculate the values between the measured ones. It is easy to include in the simulation program as well. Judging from the smooth change of the specific heat, for example, it is assumed that we can calculate the regression equations. Please let me skip the mathematical evaluation if we can calculate the regression equations. |
| |
| Please find the regression equations, some of which are obtained from the least squares method. There are many proposals for the equations in the web as well. |
| |
 |
| Density 351.99/T(K) + 344.84/T(K)^2 |
| Viscosity1.4592 x 10^(-6) x T^(3/2) / (109.1 + T) |
| Specific Heat = 0.991149-4.910^(-6) x T^(3/2) + 4.68 x 10^(-7) x T^2 ? 1.6 x 10^(-10) x T^3 |
| (NOTE: Applicable at three hundred degrees K. and higher.) |
| Convection Heat Transfer Coefficient = 2.3340 x 10^(-3) x T^(3/2) / (164.54 + T) |
| |
 |
| (6) Temperature Dependence of Prandtl Number |
| |
 |
| |
| The Prandtl number is very convenient for the simulation and we can calculate it as defined above. |
| |
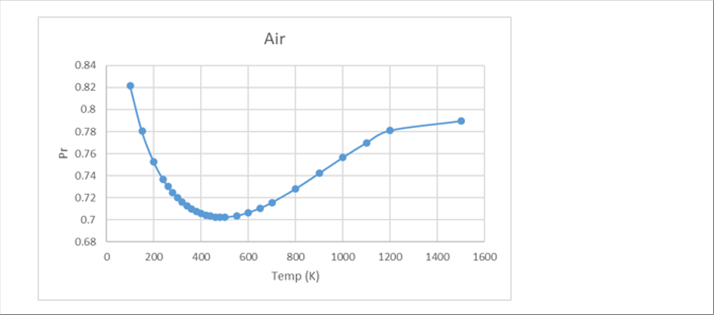 |
| |
 |
| (7) Evaluation of the Regression Equations, Density, Thermal Diffusivity and Viscosity |
| |
| The following three (3) charts show the comparison between the measured and the calculated ones. The angles show forty five (45) degrees, which means good correlation. Please let me skip the mathematical evaluation. |
| |
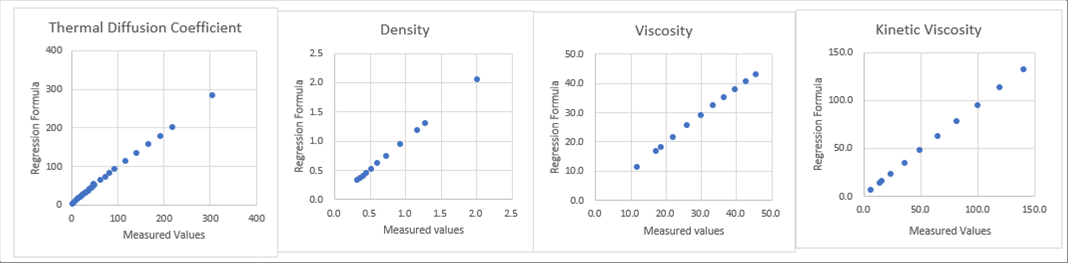 |
| |
 |
| (8) Evaluation of the Regression Equations, Specific Heat |
| |
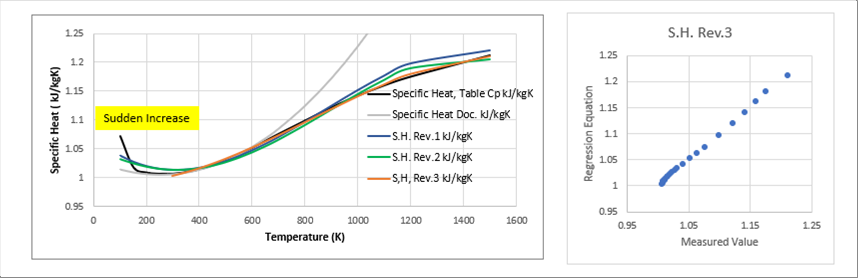
| The specific heat is an independent variable and one of the most important indexes. Therefore, there are many proposals of the regression equations. The following graph shows the measured ones and several proposals, found in the web. |
| |
 |
| |
| The measured one shows the sudden increase below one hundred and fifty (150) degrees K. It gradually increases and reduce the increase rate at about eleven hundred (1100) degrees K. Therefore, it is very hard for a regression formula to cover the whole temperature range. |
| |
| However, if we need the values for the room temperature and higher, we may ignore the behavior at lower temperature. |
| |
| For example, please take a look at the rev.3 regression equation. As long as the temperature is higher than three hundred (300) degrees K., it shows a good correlation. |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and automatic html and css generation by the "excel2web". |
| |
| |
| |
| |
| |
| |
| |
| |



































