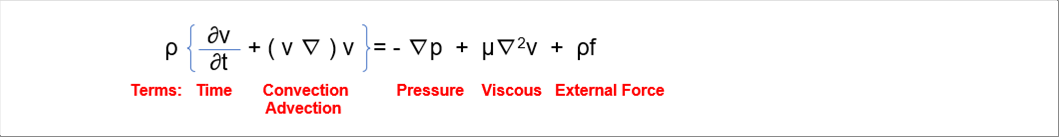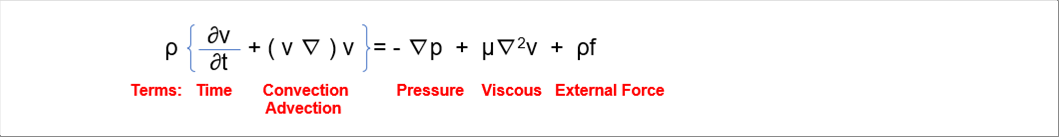| |
 |
| |
 |
| 1 Fluid Mechanics as Production Sites |
| 2 Fluid Mechanics is Complex. |
| 3 Definition and Meaning of Terms |
| 3-(1) Viscosity and Kinetic Viscosity |
| 3-(2) Effect of Temperature on Viscosity and Kinematic Viscosity |
| 3-(3) Viscosity and Kinematic Viscosity of Air at High Temperature |
| 3-(4) Reynolds Number |
| 3-(5) Laminar Flow and Turbulent Flow |
| |
 |
| 1 Fluid Mechanics as Production Sites |
| |
| At home, we use various home appliances, air pumps, high-pressure washers, etc. The author thinks there are many devices that work by using the properties of air and water. |
| |
| At the production sites, we use more powerful version of those we use at home. If much more powerful ones are necessary, we install adequate pumps. |
| |
| Air and water are called fluids, and since fluids deform or change shapes freely, no knowledge is necessary to deform them. However, since fluids are used to transmit power, heat, and other form of energy, it should be interesting to know what happens to fluids. |
| |
| A wide variety of fluids are used at production sites. For examples, air conditioners handle gases and water, furnace-related ones manage fuel gas, compressed air, combustion gas, etc. Items used in production equipment include compressed air, cooling water, hydraulic oil, lubricating oil, descaling water, cutting water, etc. |
| |
| When maintaining, managing, and improving equipment and operations, it is important to understand the basics of fluid mechanics, because they are useful especially when performing experiments and tests are difficult. They are also useful when considering and analyzing test or operating results. Therefore, it should be significant. |
| |
 |
| 2 Fluid Mechanics is Complex. |
| |
| The load on a solid object can be roughly divided into two (2) types. One is static loads such as an apple placed on a table, and dynamic one such as when you hit a home run. Dynamic loads may be applied repeatedly and are further classified into several types depending on whether they are from zero (0) to peak value, or from negative value to peak one. Hammering on a nail may be an example of the former one, and vibrations of a car engine is an example of the latter one. |
| |
| Once we know the load on a solid object, we can create an equation of motion for the object. |
| |
| Regarding fluid motion, it is necessary to consider the properties and conditions of fluid in addition to the load applied to the fluid. This is why fluid mechanics is complex. |
| |
| There are two (2) types of fluid/ incompressible fluid (liquid) and compressible fluid (gasses). There are three (3) types of flow states: laminar flow (low speed), turbulent flow (high speed), and the transition one between them. Therefore, the differential equation of motion vary by property and by state. The author does not think there is an equation that expressed them all at once. (The author did not know when s/he was a student.) |
| |
| When the fluid is air, it becomes even more complex because key indexes such as viscosity, density, and specific heat are temperature dependent. |
| |
| The equation of motion of fluid is the Navier-Stokes equation. How to derive it is introduced in another page, so please refer to it. Here, the author would like to explain the basic knowledge of fluid mechanics and introduces some formulas and examples. |
| |
| Once you know fluid mechanics, you can understand the properties of fluids, the forces exerted on fluids, the forces on objects in contact with fluids, and their movement, etc. However, it is difficult to solve the motion equation analytically. (The author does not think that the analytical solution exist.) |
| |
| A typical example is boiling water in a kettle on a gas stove at home. The movement of the flame on the gas stove is expressed by the equation of motion of a fluid, and the phenomenon that the heat of the flame is transferred to the kettle on the surface of the kettle is describes by thermodynamics. Fluid mechanics and thermodynamics are closely related, as explained in the "Thermodynamics." |
| |
 |
| 3 Definition and Meaning of Terms |
| |
 |
| 3-(1) Viscosity and Kinetic Viscosity |
| |
| |
| Viscosity and kinetic viscosity tend to be confused because the words have similar impressions (personal impression). The author will explain them because they are important to understand the movement and behavior of fluids. |
| |
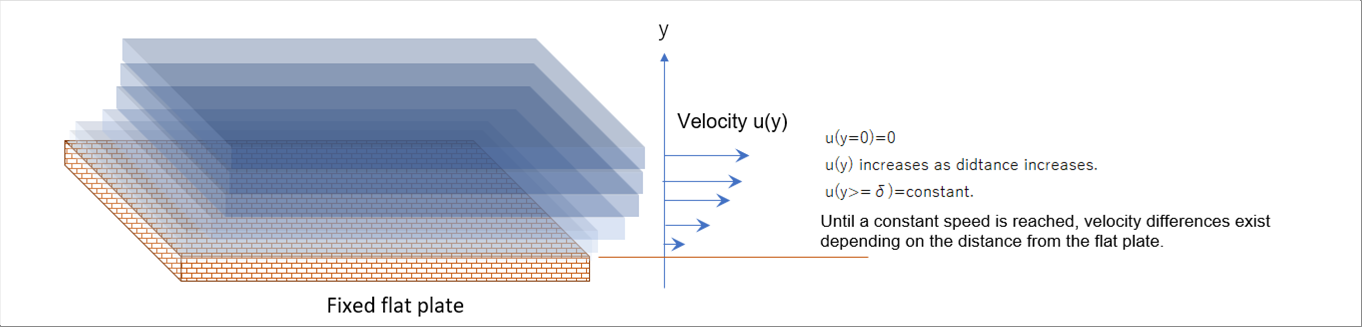
| The following picture ahpws a schematic view of fluid in a flat plate. |
| |
 |
| |
| The velocity of fluid on the surface of the plate is zero (0), and gradually increases as it moves away from it in the y direction. It becomes constant once it moves away from it to a certain extent. Until a constant velocity is reached, velocity differences exits because the velocity differs depending on the distance y. |
| |
 |
| |
| It can be assumed that the faster layer is pulling the slower one, and conversely, the slower one is braking the faster one. The pulling (braking) force is called shear force, and it is considered that the shear force is generated by the velocity difference. The shear force is assumed proportional to the velocity difference, and the proportionality coefficient is called viscosity (viscosity coefficient). This is called Newton's law of viscosity. |
| |
 |
| |
| (1) τ=μ du/dy Relationship between fluid velocity gradient and shear force [Newton's law of viscosity] |
| (2) An indicator of the ease with which force is transmited in a fluid. |
| (3) If the viscosity is big, it is difficult for the object to move, but the force caused by movement is easily transmitted. |
| (4) An indicator for the difficulty of moving an object in a fluid. |
| |
| Regarding the proportionality constant, when transmitting force using fluid, it is necessary to select an appropriate material. Let's consider the case of transmitting the same force over a long distance. Water requires large velocity to transmit shear forces over long distance, but paint can transmit same force over same distance at much slower velocities. This is very noticeable in gases, it would probably be impossible to transmit the same force over same distance in air. |
| |
| Even with the same velocity gradient (difference), the forces transmitted by air, water, and paint are vastly different. It is probable due to density as well as viscosity. It seems safe to assume that a fluid with high density can transmit a greater force than that with a fewer density. |
| |
| The viscosity divided by the density is the kinematic viscosity. |
| |
| (1) Name: Kinematic viscosity ν [m2/s] |
| (2) Definition: ν=μ/ρ (μ: Viscosity, ρ: density) |
| (3) When transmitting force to a fluid a certain distance away by its viscosity, a fluid with a high density may have a low velocity. Fluids with low density require high velocities. |
| (4) Kinematic viscosity can be said to be an index of how easily the velocity of a fluid is transmitted. |
| (5) An indicator of how difficult the fluid itself is to move. |
| |
 |
| 3-(2) Effect of Temperature on Viscosity and Kinematic Viscosity |
| |
| Temperature is an important parameter when considering fluids. |
| |
| We often see liquids in our daily lives, so we have probably experienced the effect of temperature. For example, those who drive cars of motorcycles are well aware that the viscosity of engine oil decreases as its temperature increases. When we put salad oil on a frying pan and raise the temperature, it starts flowing soon. |
| |
| Many gases are invisible to naked eyes, so the author does not think many of us have experienced what happens to their viscosity as the temperature rises. It is the opposite of a liquid: its viscosity increases. Another important thing to keep in mind is that as the temperature increases, the volume increase dramatically. Due to the effect, the density of gases decrease as the temperature increase. The density change does affect the kinematic viscosity. |
| |
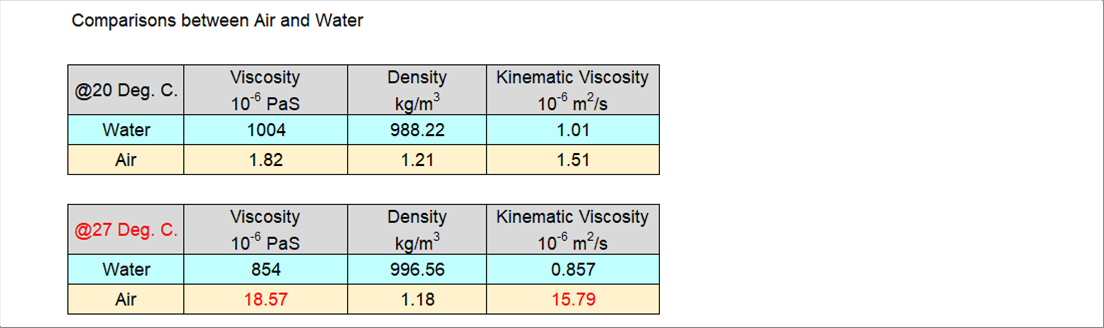
| The following two (2) tables show the comparison between water and air at temperatures of twenty (20) degrees Celsius and twenty seven (27) degrees Celsius. At 27 degrees, the density of air does not change much: however, it shows the big incrase in viscosity by about ten (10) times. |
| |
 |
| |
| |
 |
| 3-(3) Viscosity and Kinematic Viscosity of Air at High Temperature |
| |
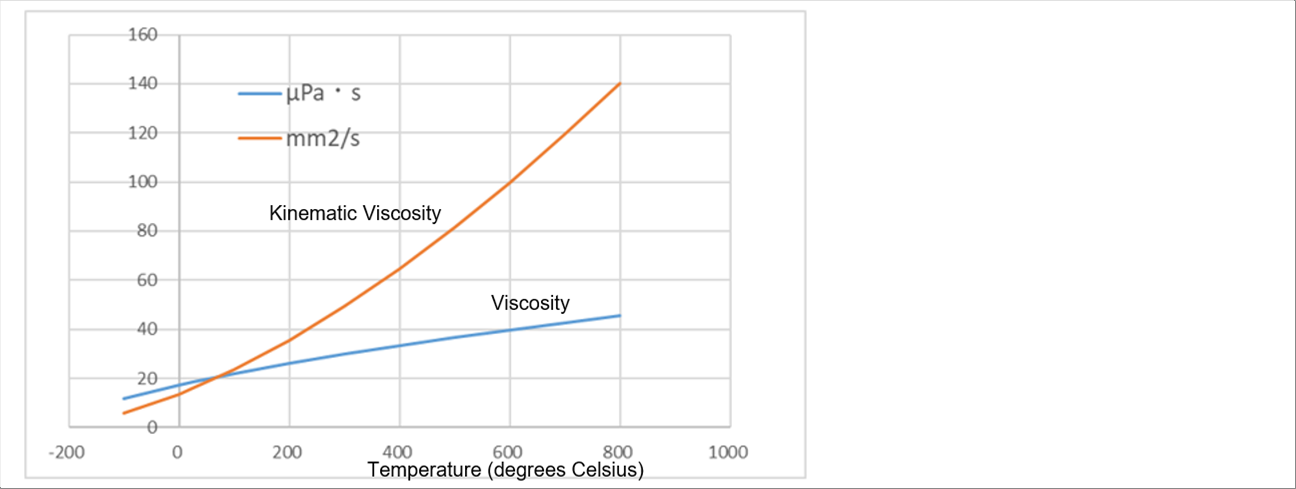
| The viscosity and kinematic viscosity of air at atmospheric pressure are as follows. |
| |
| The following graph shows the change in viscosity and kinematic viscosity due to temperature, and you can see that the viscosity and kinematic viscosity of air change greatly depending on the temperature. So, the author suggests that you use appropriate numerical values or regression equations when performing simulations. |
| |
 |
| |
 |
| 3-(4) Reynolds Number |
| |
| The Raynolds number is one of the important indicators in fluid mechanics. The flow pattern changes depending on the Raunolds number, and the formula to be applied changes. |
| |
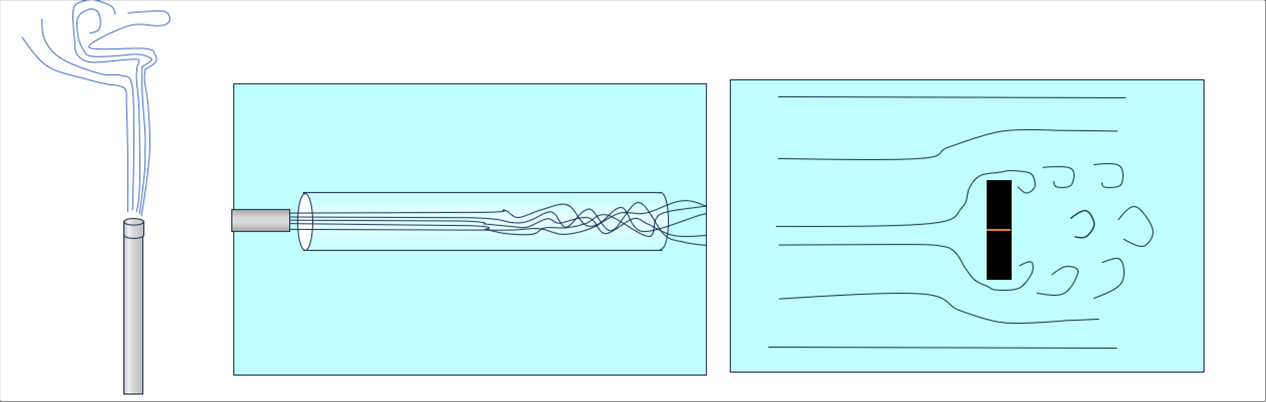
| When a river is flowing slowly, it looks smooth. When the current is fast, it looks turbulant. |
| |
 |
| |
| また、同じ速さでも、流れる距離が長くなると、下流に行くに従い、ところどころが荒れているように見えます。 |
| |
 |
| |
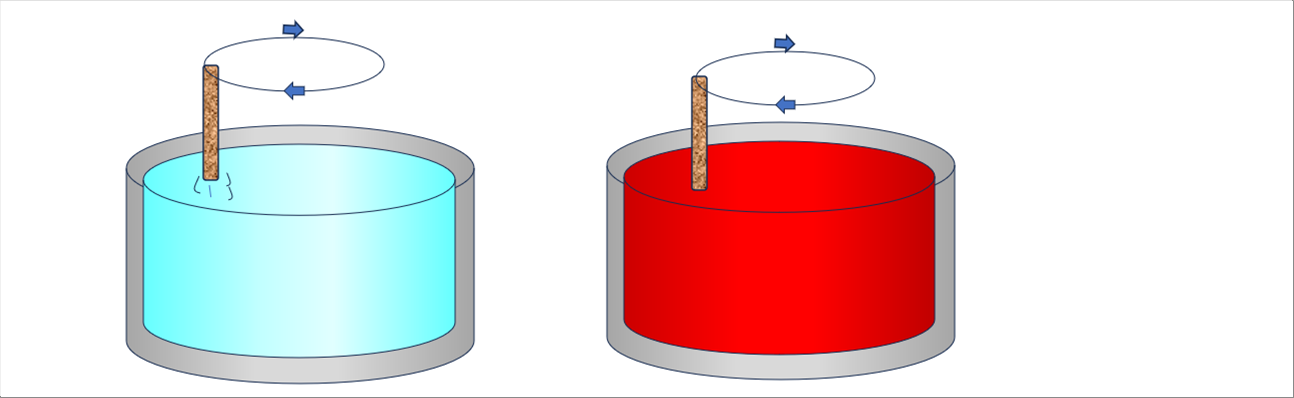
| へらを使って水を撹拌する場合とペンキを撹拌する場合では、水のほうが同じ速さでも荒れた流れに見えます。 |
| |
 |
| |
| In this way, flow conditions are believed to be influenced by dimensions such as flow path length and width, in addition to velocity, viscosity, and kinematic viscosity. The Reynolds number was proposed by our great predecessors, Stokes and Reynolds in the nineteenth (19th) century. |
| |
| (1) Indicator of influence of viscosity on flow [dimensionless quantity] |
 |
| |
| Meaning |
| a: Small Reynolds number: Laminar flow due to viscosity. |
| b: Large Reynolds number: Turbulent flow due to domination of inertial force. |
| |
 |
| |
 |
| 3-(5) Laminar Flow and Turbulent Flow |
| |
| There are significant differences between laminar flow and turbulent flow, not only in appearance but also in state and velocity. Laminar flow is a steady flow whose velocity can be describes as a function of distance from the wall. In turbulent flow, the change in velocity is not necessarily a function of distance. The velocity distribution of laminar flow is maximum at the center of the flow, and the relative velocity to the wall is zero (0) at the wall. The velocity distribution of turbulent flow is maximum at the edges and small at the center. There is also an intermediate state between laminar flow and turbulent flow, which is called transition state. |
| |
| The flow of air and water at home, manufacturing sites, etc. is usually considered to be turbulent unless it is arbitrarily laminar. For example, when you ride a bicycle at a certain speed, your clothes flap. It is because vortexes of air are created around you. Generally speaking, if you want to do something "efficiently", you would consider as the basic idea that execution should be done at a high speed. Again, moving air or water quickly results in turbulent flow. |
| |
 |
| |
| The motion of fluid can be described by the Navier-Stokes equation below. If we solve it as a stedy flow, we will get a laminar flow solution. And solving as an unsteady flow will create a turbulent solution. The equaiton cannot be solved analytically except in extremely special cases, so numerical calculations are essential. The steady-state solution can be easily calculated using a laptop. However, in order to obtain solutions for turbulent flow, a high-performance compunter is necessary. |
| |
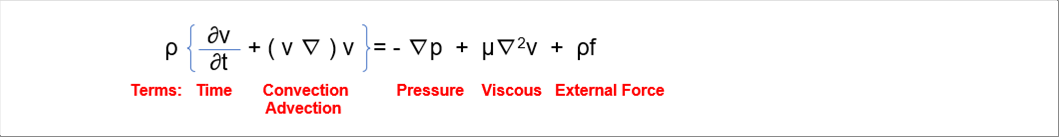 |
| |
| The author has no super computer or something like high-performance computers, so turbulent flow will be omitted in the webpage. As an example of numerical analysis, an example of calculating the temperature distribution of a pipe on a laptop is shown in "Numerical Analysis", so please refer to it. |
| |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |