| |
 |
| |
 |
| 1 Law of Conservation of Mass, Continuity Equation |
| 2 Law of Conservation of Energy, Bernoulli's Theorem |
| 2-1 Dynamic Pressure, Static Pressure, Water Head |
| 2-2 Bernoulli's Theorem involving Pressure Loss |
| |
 |
| 1 Law of Conservation of Mass, Continuity Equation |
| |
| The law of conservaion of mass holds true for fluid flow. The general formula including compressible fluids as follows. |
| |
| Mass passed through cross section A1 is equal to mass psssed thrugh cross section A2. |
| |
 |
| |
| For imcompressible fluids; |
| |
 |
| |
 |
| 2 Law of Conservation of Energy, Bernoulli's Theorem |
| |
| (1) The energy on the streamline in the fluid is constant. |
| (2) Kinetic energy + pressure energy + potential energy = Constant |
| (3) For compressible fluid, the internal energy changes, but for incompressible fluid, the internal energy does not change. (Therefore, the internal energy can be omitted.) |
| (4) From here, we consider steady flow of incompressible fluid. (no vortex) |
| |
 |
| 2-1 Dynamic Pressure, Static Pressure, Water Head |
| |
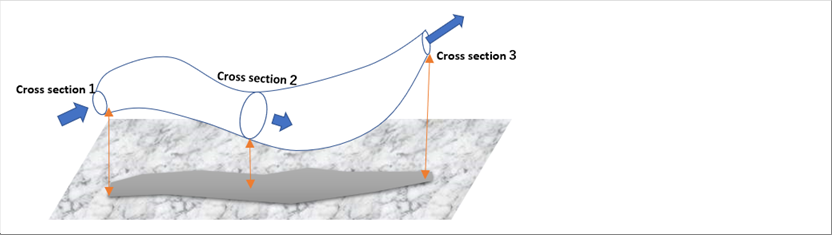
| In a streamline (flow path), the sum of static pressure, dynamic pressure, and potential energy is constant. It is the law of conservation of energy, which is called Bernoulli's theorem. It was proposed by Bernoulli in eighteenth (18th) century. |
| |
 |
| |
 |
| |
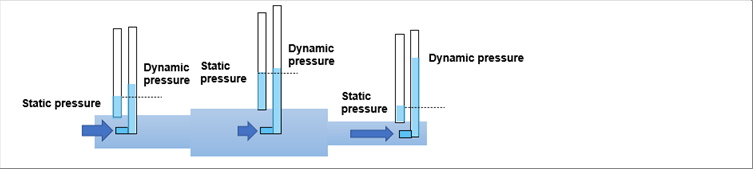
| As shown in the following picture, if we put a glass tube in each position where static and dynamic pressures can be measured, and look at them, each glass tube indicates the ligiid level corresponding to the pressure at each position. |
| |
 |
| |
| When the pressure is expressed in terms of water heads, divide the formula of Bernoulli's theorem by ƒÏg. Pressure head + velocity head + positioni head = constant 2. |
| |
 |
| |
| Static pressure P => Pressure head P/ƒÏg |
| Dynamic pressure 0.5ƒÏv^2 => Velocisy head 0.5v^2/g |
| |
 |
| 2-2 Bernoulli's Theorem involving Pressure Loss |
| |
| In the actual flow, there is a pressure loss due to viscous friction of the fluid, etc. and it may be large enough to be ignored. Therefore, confirmation is necessary. When we express the formula in water head, it is given by; |
| |
 |
| |
| If the points lie on the same horizon, the potential energies are identical. Furthermore, when the points are in the same flow path, the velocities are also the same. And then, the pressure loss is defined by; |
| |
 |
| |
| (Please refer to the "Pressure Loss" for detail.) |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |



























