| |
 |
| |
 |
| (1) What is the Finite Element Method? |
| (1)-1 Advantages of the Finite Element Method |
| (1)-2 Important Notes |
| (2) Differential Calculus and Finite Element Method |
| (3) Application of the Finite Element Method |
| (3)-1 An Example, Application to the Structural Analysis |
| (3)-1-a Variables and Equations |
| (3)-1-b Boundary Conditions |
| (3)-1-c Various Kinds of Meshes (Elements) |
| (3)-1-d Adequate Elements |
| (3)-1-d-a Elastic and Plastic Deformations |
| (3)-1-d-b Aspect Length-to-Width Ratio |
| (3)-1-d-c Size of Elements |
| (3)-2 Calculation |
| (3)-3 Validation of the Outcome |
| (4) Developments |
| |
| |
 |
| (1) What is the Finite Element Method? |
| |
| Please see the "Numerical Analysis" in the "Technical Stories" as well. |
| |
| The finite element method (FEM) is applicable to every field. In addition, it has a lot of flexibilities, and the outcome is very precise. In order to enjoy those advantages, knowledge for the specialty fields is necessary. There are many papers and reports from many universities, laboratories, and related associations. For example, The Institute of Industrial Science, the University of Tokyo opens the papers about the metal plastic deformation and heat transfer. Therefore, please see those sources for detail. |
| |
 |
| |
| Here, let's focus on the points in order to understand what it is. The numbers of should be as few as possible. There are four (4) major points in the FEM. |
| |
| (1) It is an approximate solution of the deferential equations. |
| (2) Therefore, the inevitable errors are generated. |
| (3) The area of the analysis is divided into mesh (elements). |
| (4) It is to apply and to solve the simultaneous equations of the elements. |
| |
| The error, describe in (2), can be minimized to meet the purpose of the analysis. |
| |
| The mesh, in (3), are up to you; however, the seize, the type, the numbers of the elements do affect the outcome. |
| |
| The simultaneous equations, in (4), are also up to you. For example, the experimental formula are OK. It sounds easy; however, it does affect the outcome. |
| |
 |
| (1)-1 Advantages of the Finite Element Method |
| |
| I am afraid that it is widely utilized nowadays, and therefore, (1) it can be used as a Blackbox in a good meaning. |
| |
| (2) It is applicable to the complex shape and the precise outcome can be obtained. (NOTE: the difference method can also be applied to the complex one as well.) |
| |
| FEM gives the so-called "average" value of each element. Therefore, the extrapolation method is used for the values of the vertex of the elements. The boundary conditions, such as external load and friction force, are applied to the surface of the material. Therefore, the extrapolation is very important to apply the boundary conditions. |
| |
 |
| (1)-2 Important Notes |
| |
| There are three (3) important notes for the FEM. Fist of all, the shape, the size and the number of the mesh (element) shall be adequately defined. Then, the formula applied to the inside of the mesh shall be solvable. Lastly, it is necessary for the analysis to evaluate the outcome. |
| |
| When you use the FEM as a Blackbox, the outcome gives many kinds of indexes. You can utilize those for the evaluation. For example, if you use it to the structural analysis, it may give you the hVon Mises Stress" as well ad the stress distribution. You can use the Mises stress if it meets the reality of the deformation. (Please see the "Material Dynamics" for the Mises stress.) |
| |
 |
| (2) Differential Calculus and Finite Element Method |
| |
| The difference method is the direct approximate of the differential equations by using the Taylor expansion. However, I think it is not mandatory for the FEM to be connected to the differential equations. You can select the best substitution. |
| |
 |
| (3) Application of the Finite Element Method |
| |
 |
| (3)-1 An Example, Application to the Structural Analysis |
| |
| Let's consider the application to the structural analysis as an example, because it is frequently used. |
| |
 |
| (3)-1-a Variables and Equations |
| |
| The stress and strain are what we need to know in the structural analysis. As a basic of the mathematics, the simultaneous formula are solved if the numbers of the valiables and the formula are same. There are three (3) available equations in the structural analysis. |
| |
| (1) Equilibrium formula of forces |
| |
| (2) Dislocation (position change) and strain relational equations |
| |
| (3) Stress and strain relational equations |
| |
| These formula are applicable to each element. The force equilibrium at the boundary gives the strain. The strain can be converted to the dislocation of the element. It can be connected one after another within the whole area. Therefore, you can calculate the stress and strain for whole area. (Please see the "Material Dynamics" for the detail formula.) |
| |
 |
| (3)-1-b Boundary Conditions |
| |
| One of the examples of the external forces is the following tension to the bar, like the tensile testing. Both of the ends are clamped, the load is applied and is measured to the bar under the constant strain rate. Another example is the force of the typhoon wind, which blows a house. The direction and speed of the wind is changed in order to know if the hose can stand against the wind. These are the conditions, which are applied at the boundary between the forces and the material, and it is called the "boundary conditions". |
| |
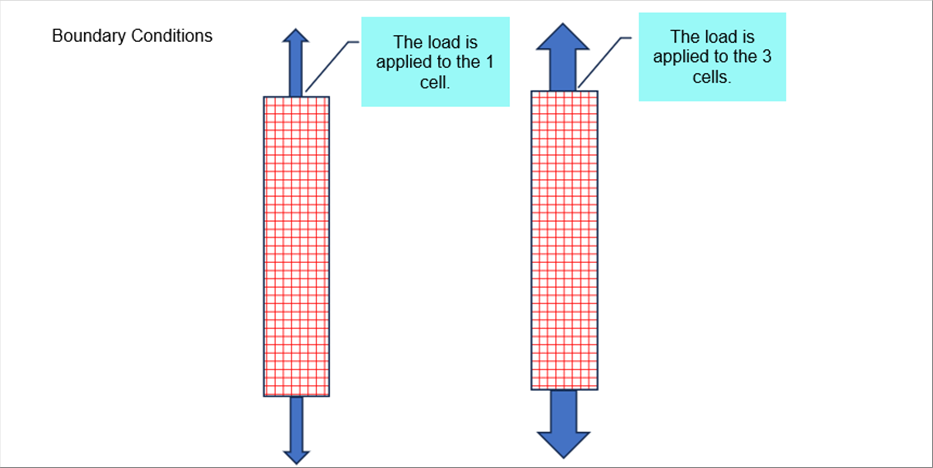 |
| |
| As seen in the above picture, how to apply the load is very important. The same "concentrated" load can be applied either to a cell or to three (3) cells. |
| |
| The "concentrated load" and the "distributed load" are easy to write in texts. For example, "The concentrated load of 1 N is applied from an inch from the end of the beam A." The question is how to express the text in the FEM. The FEM is very flexible and whatever the condition can be applied. it is necessary to determine the condition in detail. The direction of the force may be perpendicular, 3 elements may receive the force. Depending on the boundary condition, the outcome can be different. |
| |
 |
| (3)-1-c Various Kinds of Meshes (Elements) |
| |
| The above example was the tensile testing, which is one-dimensional (1D). Honestly speaking, the FEM is seldom used for such 1D ones. On the contrary, FEM is applied to either 2D or 3D ones. There are many kinds of elements. The following pictures show some of the examples of them. |
| |
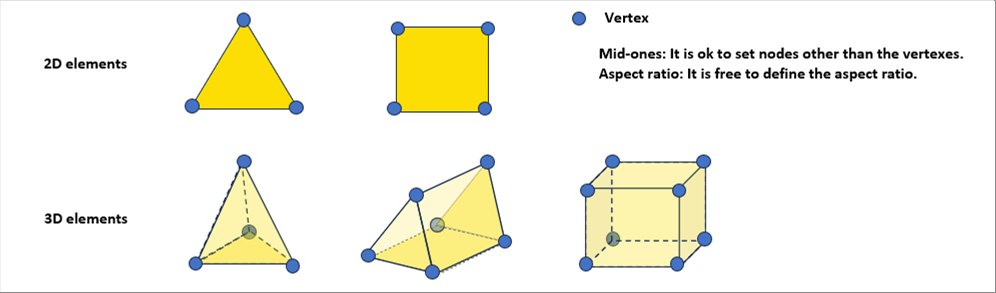 |
| |
 |
| (3)-1-d Adequate Shape of the Elements |
| |
 |
| (3)-1-d-a Elastic and Plastic Deformations |
| |
| The analyst can decide which types of elements to use; however, in many cases, the triangle one is used for the elastic deformation, and rectangular for the plastic deformation. |
| |
| Elastic deformation: Triangle elements |
| |
| Plastic deformation: Rectangular elements |
| |
 |
| (3)-1-d-b Aspect Length-to-Width Ratio |
| |
| The analyst can decide the aspect ratio and the angle of the elements. The following pictures show the same load is applied to five (5) different elements. The outcome may or may not represent the reality. |
| |
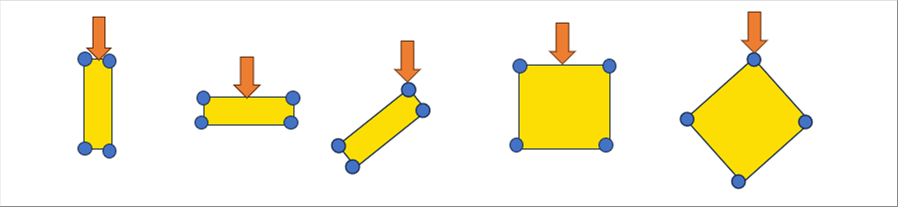 |
| |
 |
| (3)-1-d-c Size of Elements |
| |
| One of the advantages of the FEM is the mesh generation. If you are a super-person for the mesh generation, you may need only (1) time to obtain the best outcome. However, you can change as many times as you need. If the outcome is not representing the reality, you may need to change it. As a general tule, it may be suggested to start from the rough mesh generation, and then, after evaluation of the outcome, the finer ones may be necessary to the area, which is far from the reality. |
| |
| The following pictures show the different mesh generations. If you already know that the peninsula on the right bends toward downward, the right end mesh may be adequate. |
| |
| if you do not know which of the part changes, you can adopt the left end one for the quick viewing of the outcome. It may show you the stress (and strain) concentrates on the second cell of the peninsula. Then, the finer mesh may be added to the cell. |
| |
| It is also ok to start the calculation as fine as possible like the middle one. |
| |
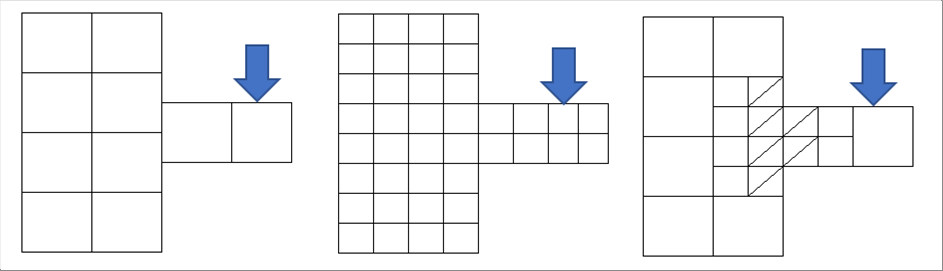 |
| |
| The coordinates of the nodes are expressed according to the coordination system, like (x, y). If we adopt the two-dimensnal (2D) rectangular coordinate system, the coordination fof the n-th node is shown as (xn, yn), and (xn, yn zn) in 3D one. |
| |
| You may use a laptop for the calculation. Each element and each node shall be numbered for the laptop to be able to execute the calculation smoothly. |
| |
 |
| (3)-2 Calculation |
| |
| It is necessary to solve the simultaneous equations in the elements. If the mesh generation is each three (3) elements in two (2) axis, the total number of elements are nine (9) and sixteen (16) nodes. If it is 2D, there are thirty two (32) unknown values. It means, it is necessary to solve the simultaneous equations in 32 unknowns. The following illustration, it is necessary to solve the simultaneous equations of five hundred and sixty (560) unknowns. In order to help such calculation, you can utilize the formula of the linear algebra. Because, if you pick up the coefficients of the simultaneous equations and the boundary condition in the matrix, you can apply the formula to get the solutions. Therefore, the matrix formula are frequently seen in the FEM. |
| |
| It is necessary to "calculate the formula, which are applied to the elements, through the material". It can be said as "volume integral". So, if the formula, which is applied to the elements, are easy to the integral, you will be able to obtain the solution easily. (Please see the "basic calculus" for reference.) |
| |
| If the internal equations are hard to integral, it is suggested to use the numerical integral. The Gauss?Legendre formula is suggested for the purpose. It generates an error; however, if you calculate the fourth-order, it becomes very small. (Please see the "Numerical Integral" for detail. ) |
| |
 |
| |
| Lastly, the formula are averagely applied to the elements. The solutions are also "average" value of each element. On the other hand, the boundary conditions are applied to the nodes. In order to connect the "average" one and the boundary conditions, the extrapolation formula are used to calculate the values of the nodes. Therefore, the extrapolation matrix also appear in the FEM formula. |
| |
 |
| (3)-3 Validation of the Outcome |
| |
| Let's assume that you obtained the outcome as the positions of nodes. The strain can be calculated by the dislocations of the nodes. Then, stress can be calculated by the stress-strain curve. Then, the stress times the area gives the force or the load. Finally, it is possible to obtain the torque (power) when the torque arm are multiplied. |
| |
| One of the ways of the validation is to compare the outcome and what we can measure. |
| |
| For example, the comparison between the outcome and the stress of the representing points by the strain gauges. The comparison of the roll separating force and the calculated one is also ok. |
| |
 |
| (4) Developments |
| |
| I may be wrong from the mathematics viewpoint, please let me propose a formula in order to summarize the above things. |
| |
 |
| |
| In addition to the analysis of the structure, the finite element method is actively used in the analysis of the thermal fluid, the heat conductivity, the hot rolling processes, and so on. The applicable differential equations for those are not solved neither. The boundary conditions are known. The formula for the elements are also proposed in many papers, and you can utilize them as well. Homepage of TS Consulting also shows some of them. Please see the "thermodynamics", "fluid dynamics", and "deformation processing" for detail. |
| |
| The structure analysis is also available in the CAD programs. There are some FEM programs, where the mesh generation is automatically done. It is very convenient. As far as I know, it is necessary for the analyst to do the final evaluation. |
| |
| It may be necessary for the analyst to define if the structure is deformed during the evaluation. The stress - strain curve or the yield criteria tells the condition, which are explained in the "deformation processing." You can select the most adequate criterion from the maximum primary stress yield criterion, from the Tresca one, from the von Mises one, or from the equivalent flow stress. |
| |
| Thanks to the flexibility of the FEM, you may use it for the failure analysis. For example, let's assume an equipment failed. You can change the external force, the friction coefficient, movement speed or acceleration, to know the yield condition of which part of the equipment increases. |
| |
| |
| |
| Author : T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |

















































