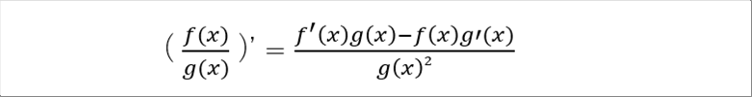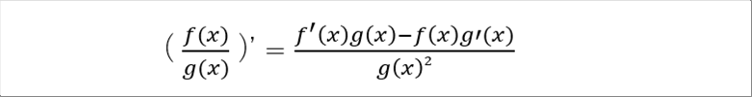| |
|
 |
|
| |
|
 |
|
| (1) Reasons why the calculus is in the stories. |
|
| (2) Example of the integral, the Second Moment of the Area (Area Moment of Inertia) |
|
| (2)-1 integral of the Trigonometric Functions to the Fourth Power |
|
| (2)-2 Half-Angle Formula, The Standard Tactics for the Trigonometric Functions to the Second Power Or More |
|
| (2)-3 Sum and Difference Formula of the Trigonometric Functions |
|
| (2)-4 Variable Substitution, integral of the Composite Functions |
|
| (3) differentiation of the Composite Functions |
|
| Differentiation of the Division |
|
| (4) How to Remember the Calculus Formula of the Trigonometric Functions |
|
| Summary of the Calculus Formula, Trigonometric Formula |
|
| (5) Differentiation of the Logarithm 1/x |
|
| (6) Differentiation of the Exponential Function (a^x)' = (a^x) log a |
|
| (7) An Example of the integral, Solving Heat Conduction Equation |
|
| |
|
| Sum and Difference Formula of the Trigonometric Functions |
|
 |
|
| |
|
 |
|
| (1) Reasons why the calculus is in the stories. |
|
| |
|
| TS Consulting will not work for the mathematics and therefore you will see the summary of the calculus. As long as you can use the calculus, you can follow all of the theories, such as the material dynamics, the thermodynamics, the fluid dynamics, and so on. The flow of calculus are shown in this article. Please skip the article if you already know them. |
|
| |
|
| We may easily forget the calculus of the trigonometric functions and of the logarithm. However, they are frequently used in the basic theories of the material dynamics. For example, the area moment of inertia is very important to calculate the stiffness of the column. |
|
| |
|
| The sum and difference formula of the trigonometric functions are easy to understand by viewing the unit cirlce. |
|
| |
|
 |
|
| (2) Example of the integral, the Second Moment of the Area (Area Moment of Inertia) |
|
| |
|
| An example, which is obtained by the calculus of the trigonometric formula, is the solution of the second moment of the area (area moment of inertia). The definition of the area moment of inertia is as following. The polar coordination system is useful for the round shape. The definition of the area moment of inertia to the small area is integrated though the area. |
|
| |
|
| The area moment of inertia around the x-axis is integral of the y squared. As seen in the following picture, y is expressed by both radius and the angle. |
|
| |
|
 |
|
| |
|
| The definition is very simple. But when we substitute b and y to the definition, we will see the trigonometric functions to the forth power. |
|
| |
|
 |
|
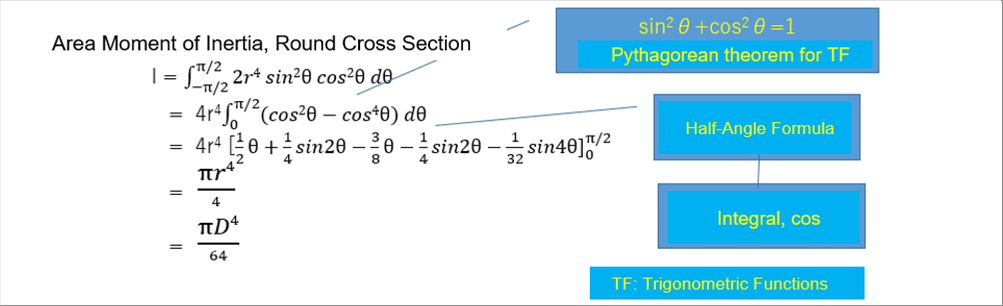
| (2)-1 integral of the Trigonometric Functions to the Fourth Power |
|
| |
|
| After the substitution, the area moment of the inertia of the round shape is obtaned. As seen in the second line of the following formula, there is a cos to the fourth power. However, the known calculus formula for the trigonometric functions are the first power. |
|
| |
|
 |
|
| |
|
| The cos to the fourth power is converted to the first power by the half-angle formula. One of the standard tactics of the trigonometric functions is to use the half-angle formula to the second power one by one to obtain the first power. |
|
| |
|
 |
|
| |
|
 |
|
| (2)-2 Half-Angle Formula, The Standard Tactics for the Trigonometric Functions to the Second Power Or Higher |
|
| |
|
| It is the standard and the most important tactics of the treatment of the trigonometric functions to use the hafl-angle formula when you face the trigonometric formula to second or higher power. |
|
| |
|
 |
|
| |
|
 |
|
| (2)-3 Sum and Difference Formula of the Trigonometric Functions |
|
| |
|
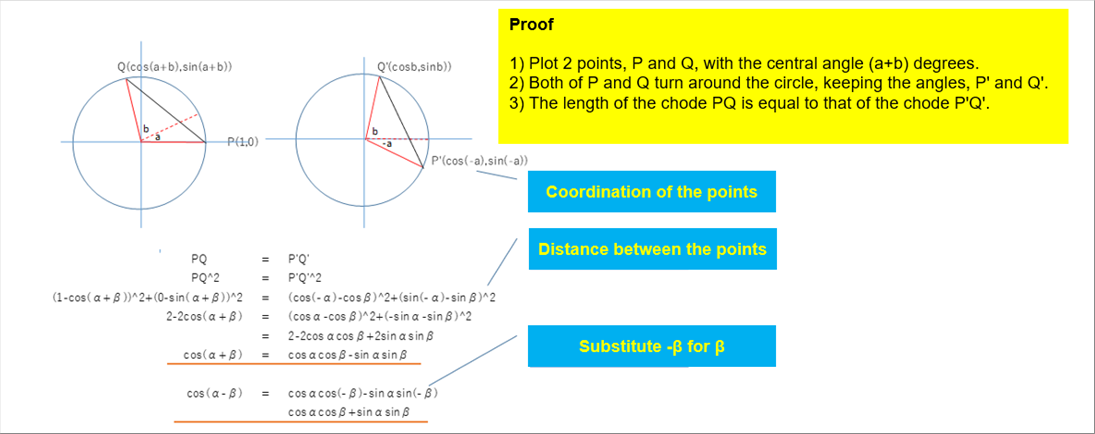
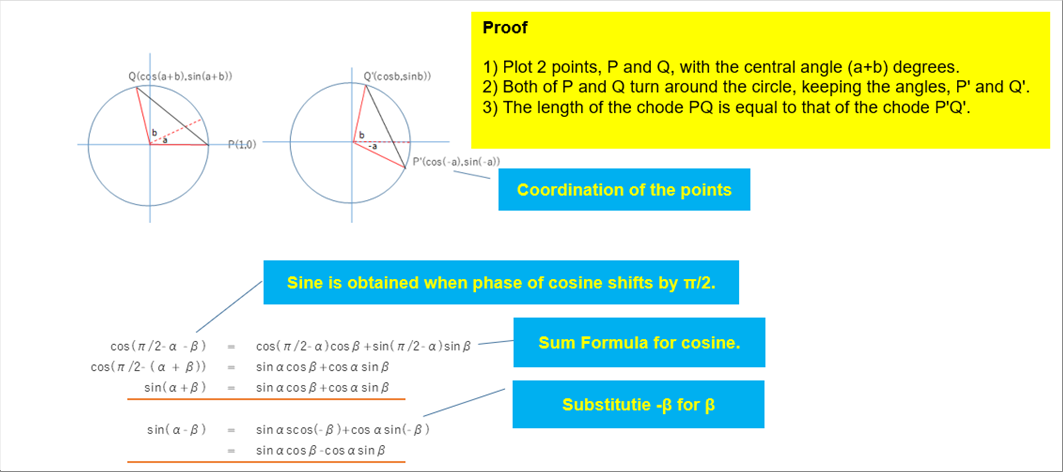
| It is easy to understand the Sum and Difference Formula of the Trigonometric Functions by the drawing of a circle. The distance between the two (2) points on the circle remains same when the 2 points move on the circle, keeping the same angle in between. |
|
| |
|
| Even if you understand the sum formula of the trigonometric functions, all of the rest of the formula can be obtained, including the calculus. However, as said in the above section the half-angle formula is highly recommended to remember, because it is very useful. Please see the last part of the article for the detail of the sum and difference formula of the trigonometric functions. |
|
| |
|
 |
|
| (2)-4 Variable Substitution, integral of the Composite Functions |
|
| |
|
| There is a fomulus for the cos a and nothing for 2a. The substitution is useful (necessary and sufficient) for the calculation of the double angle, 2a. |
|
| |
|
| In order to use the integral formula, let's assume 2a = b. It is the substitution, and then, we can use the formula. In other words, we are utilizing both of the substitution and the formula at the same time. As we are combining the two (2) things, the integral of the method is called the integral of the composite function. |
|
| |
|
| It is very much frequently used to substitute the variables and the integral of the composite functions. |
|
| |
|
 |
|
| |
|
 |
|
| (3) Differentiation of the Composite Functions |
|
| |
|
| Let's assume y=f(u) is given, and due to any reason, when we substitute the value u to u=g(x), y=f(g(x)) is defined as the composite function. |
|
| |
|
| As seen above, cosine (double angle) is one of the composite functions. |
|
| |
|
 |
|
| |
|
| That is what I like the most, because it is easy to use and I face the same issue many times. |
|
| |
|
 |
|
| |
|
| The point is to add the same thing to both of the denominator and the numerator. |
|
| |
|
 |
|
| Differentiation of the Division |
|
| |
|
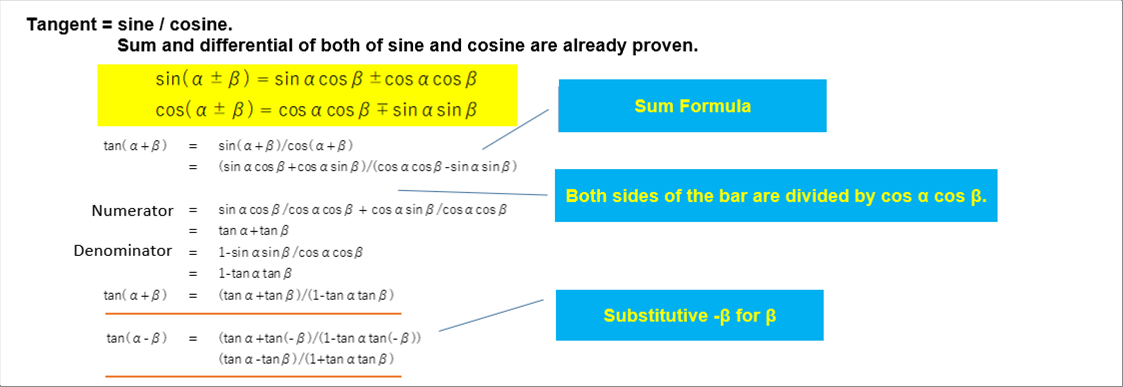
| It is necessary for the calculation of the differentiation of the tangent. Because, the tangent is defined as sine divided by cosine. |
|
| |
|
| 小の微分の公式は下記です。これは、微分の定義である導関数を変形すると導くことができます。 |
|
| |
|
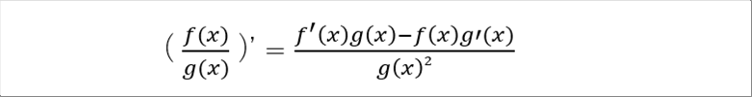 |
|
| |
|
 |
|
| |
|
| The point is to subtract and to add the same item. |
|
| |
|
| The methods, one is to add the same item to both sides of the bar, and another is to subtract and to add the same item to either side of the bar, are used in the deferential equations, as well. |
|
| |
|
 |
|
| (4) How to Remember the Calculus Formula of the Trigonometric Functions |
|
| |
|
 |
|
| |
|
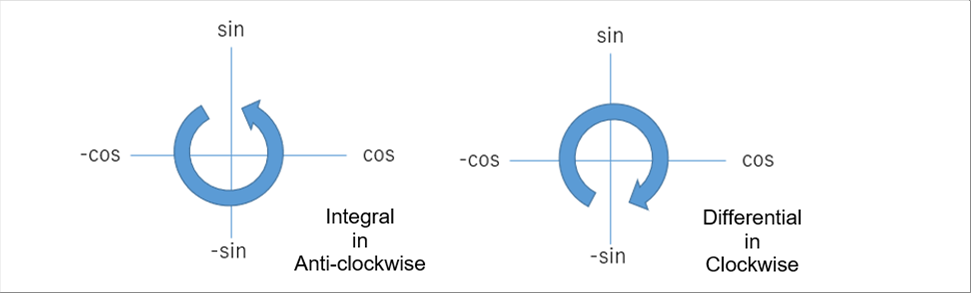
| When draw the sine and the cosine as following, the integral is in the anti-clockwise, and differentiation in the clockwise. |
|
| |
|
 |
|
| |
|
 |
|
| Summary of the Calculus Formula, Trigonometric Formula |
|
| |
|
 |
|
| |
|
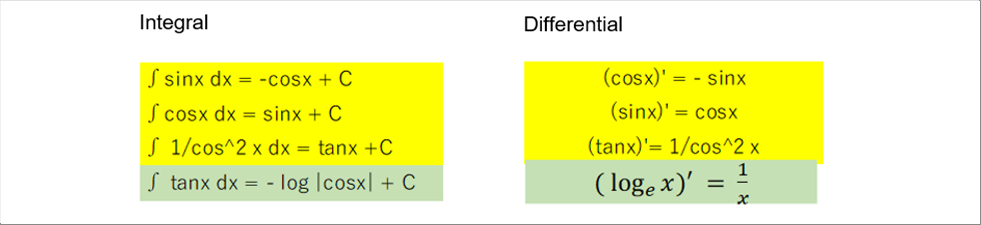
| As seen above, both of the integral and differentiation of sine and cosine are cyclically calculated. While tangent is out of such cyclical change. |
|
| |
|
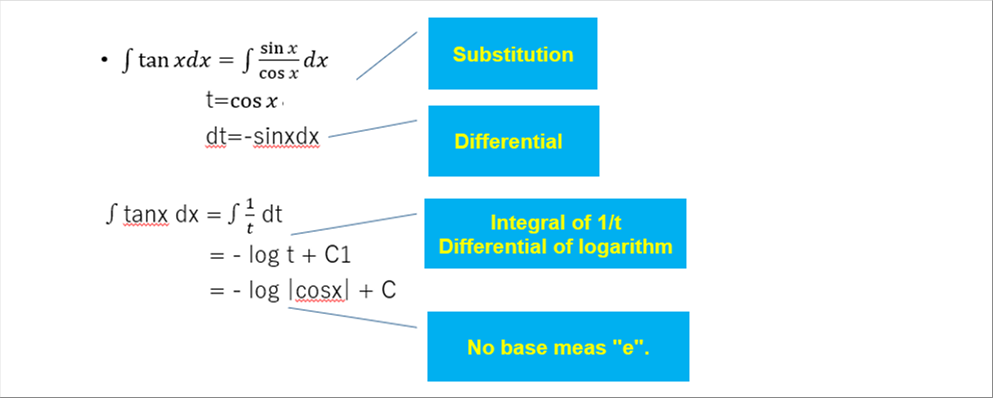
| The integral of tan x simply becomes that of 1/t when we substitute cos x = t. The differentiation of the natural logarithm is 1/t, and therefore, the above formula is obtained. |
|
| |
|
 |
|
| |
|
 |
|
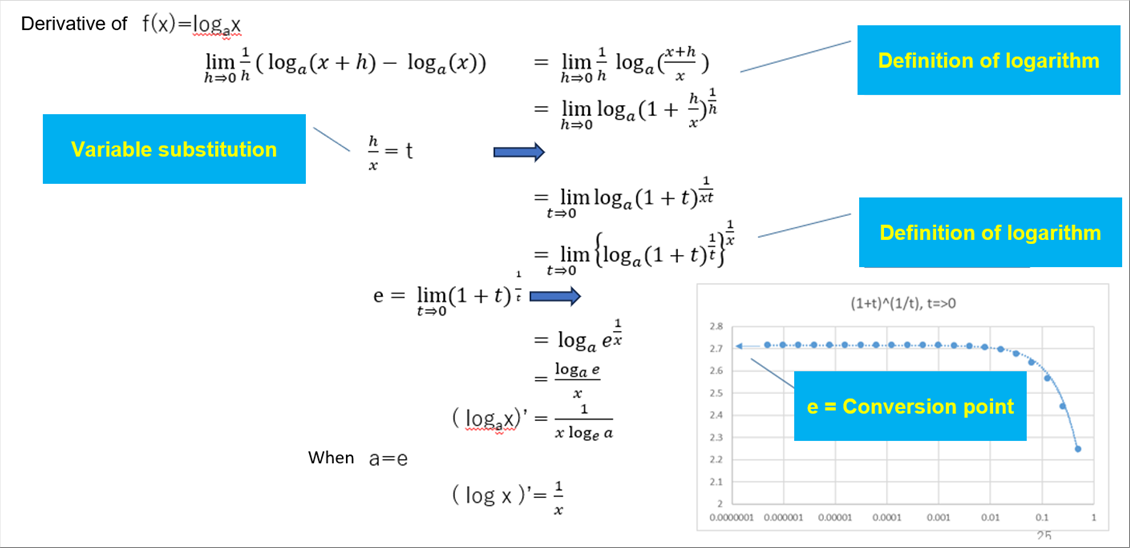
| Differentiation of the Logarithm is 1/x. |
|
| |
|
| It is as following. |
|
| |
|
 |
|
| |
|
 |
|
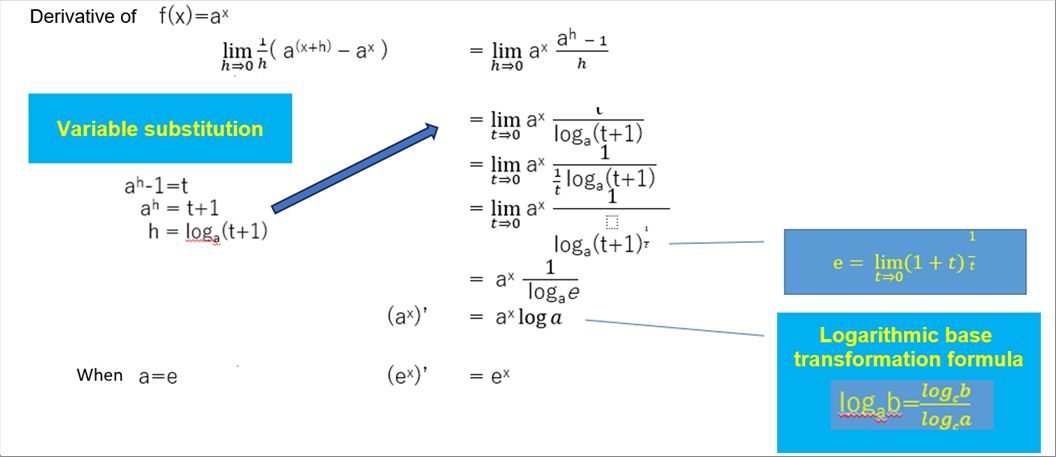
| (6) Differentiation of the Exponential Function (a^x)' = (a^x) log a |
|
| |
|
| The differetiation of the exponential function is the exponentioal function. |
|
| |
|
 |
|
| |
|
| The differentiation of a^x is different from that of x^a. It is confusing, but if you forget it, you can recover if from the calculation of the derivative. |
|
| |
|
 |
|
| (7) An Example of the integral, Solving Heat Conduction Equation |
|
| |
|
| We cannot solve the heat conduction equation analytically. (Please see the thermodynamics for detail.) |
|
| |
|
| Only when the heat conduction equitation is expressed to u(x,t)=T(t)X(x), it can be solved analytically. The solution contains no error; however, the physical meaning of the expression is too simple. It means the long bar with both ends are kept zero (0) degrees C., for example. |
|
| |
|
 |
|
| Sum and Difference Formula of the Trigonometric Functions |
|
| |
|
| The formula are easy to understand when we see the unit circle. |
|
| |
|
| cos ( a 土 b ) = cos a cos b 干 sin a sin b |
|
 |
|
| |
|
| sin ( a 土 b ) = sin a cos b 土 cos a cos b |
|
 |
|
| |
|
| tan ( a 土 b ) = ( tan a 土 ttan b ) / ( 1 干 tan a tan b ) |
|
 |
|
| |
|
| |
|
| |
|
| |
|
| Author: T. Oda |
|
| The page was prepared in Excel, and automatic html and css generation by the "excel2web". |
|